ciências

Hipócrates de Quios / As lunas

O esquema mostra as bases da solução proposta por Hipócrates de Quios para o antigo problema da quadratura do círculo, conservado por Simplício em seu Comentários sobre a Física de Aristóteles (in Phys. 69.22.-3).

Trata-se, a bem da verdade, de uma solução parcial, pois Hipócrates conseguiu comprovar somente que certas partes do círculo podem ser representadas por quadrados de mesma área.

Fig. 0052. A luna de Hipócrates de Quios.

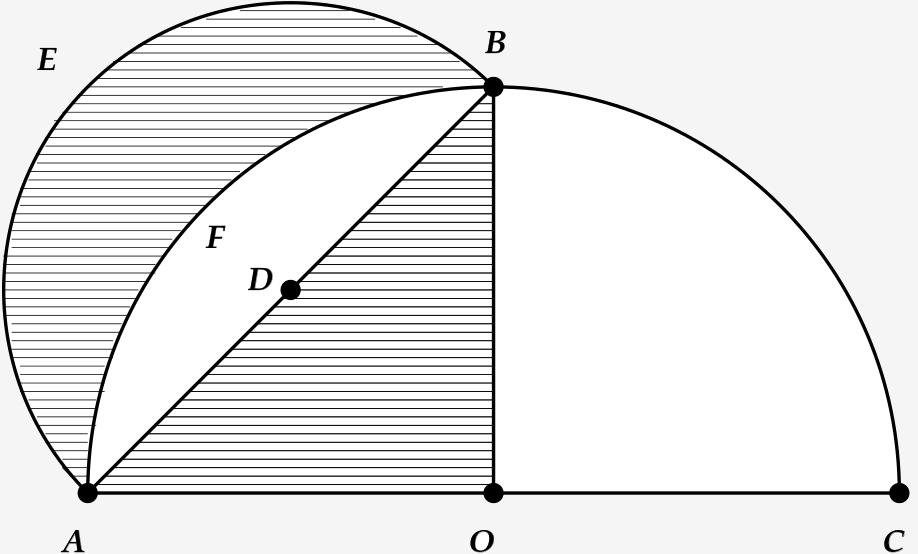
No esquema ao lado, portanto, a área da luna[1] AEB é igual à área do triângulo ABO.

A comprovação se baseia em três enunciados matemáticos bem conhecidos:

  1. o teorema de pitágoras;
  2. um ângulo incrito em um semicírculo é um ângulo reto;
  3. as áreas de dois círculos ou semicírculos são proporcionais entre si, assim como o quadrado de seus diâmetros.

Demonstração:

  • o centro do círculo onde fica o arco AEB é o ponto D, que é o ponto médio da hipotenusa do triângulo retângulo isósceles ABO;
  • o diâmetro AC do círculo maior ABC é √2 vezes o diâmetro do círculo menor, onde está o arco AEB;
  • consequentemente, o círculo menor tem metade da área do círculo maior;
  • o semicírculo em contato com o arco AEB e o diâmetro AB têm, portanto, a mesma área que o quarto de círculo em contato com o arco AFB e os dois raios OA e OB;
  • subtrair de ambos os lados dessa igualdade a área da região em contato com o arco AFB e a linha AB produz o resultado.

Veja demonstrações matemáticas detalhadas da descoberta de Hipócrates de Quios nos links externos e nas referências.