Euclides / Elementos 1.17

Euc. El. 1.17 c. -295

A tradução desta passagem, originalmente do grego para o inglês, é de Thomas L. Heath (1861/1940), ex-Secretário do Tesouro do Reino Unido, e foi publicada em 1908. A versão do inglês para o português é de minha autoria.

Proposição 17 do Livro I

Em qualquer triângulo, dois ângulos tomados juntos de qualquer maneira são menores que dois ângulos retos.

Seja ABC um triângulo; eu digo que dois ângulos do triângulo ABC tomados juntos de qualquer maneira são menores que dois ângulos retos.

Que BC seja prolongado até D [cf. Postulado 2]. Então, como o ângulo ACD é um ângulo exterior do triângulo ABC, ele é maior que o ângulo ABC, interior e oposto [cf. Proposição 16].
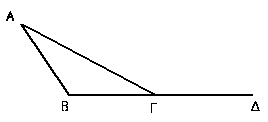
Seja o ângulo ACB acrescentado a cada um deles; portanto os ângulos ACD, ACB são maiores que os ângulos ABC, BCA.
Mas os ângulos ACD, ACB são iguais a dois ângulos retos [cf. Proposição 13].
Os ângulos ABC, BCA, portanto, são menores que dois ângulos retos.
De modo similar podemos provar que os ângulos BAC, ACB são também menores que dois ângulos retos, e assim são também os ângulos CAB, ABC. Portanto, etc., como se queria demonstrar.